Movimiento rectilíneo uniforme: La pendiente

Hasta ahora hemos visto que cuando un cuerpo se mueve desplazándose en una dirección determinada, como en el caso de la  carrera de la liebre y la tortuga, y asumimos que la distancia recorrida era positiva. Sin embargo, en un modelo podemos tener distancias con signo negativo, y en esta sección estudiaremos cómo interpretarlas.

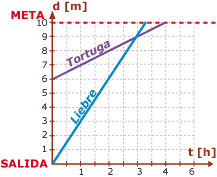
En nuestro ejemplo de la carrera, hicimos coincidir la salida con el origen. Esta gráfica modela el desarrollo de la carrera hacia la meta:

Pero ¿qué hubiera pasado si decidimos considerar como punto de origen de la gráfica la meta? En la siguiente gráfica puedes ver la representación. Observa que ahora el punto de donde salieron los animales se encuentra a 10 metros de la meta. De ese punto parte la liebre, en tanto que la tortuga se encuentra 6 m más cerca de la meta. Para modelar la carrera, recordaremos que la tortuga se mueve 1 metro por hora, es decir, por cada hora que transcurra, se moverá un metro hacia abajo, hacia la línea de meta que coincide con el eje horizontal. Por su parte, la liebre se mueve a razón de 3 metros por hora, así que su gráfica mostrará una recta que baja 3 unidades verticales por cada unidad horizontal. ¿Estás de acuerdo? ¿Qué hacer para representar simbólicamente que la distancia que recorren va en sentido contrario al de la flecha del eje vertical?

¡Claro! ¡Para eso está el signo negativo! Escribamos entonces las rapideces para este modelo:

Para la tortuga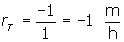

Para la liebre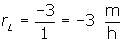

Lo cual permite ver que no sólo podemos representar móviles que se mueven en la misma dirección, sino que también pueden modelarse situaciones en las que los móviles se desplacen en direcciones contrarias e incluso, en ciertos casos, se encuentren en algún punto de su recorrido. Lo único que no es válido en este tipo de modelos es que el tiempo sea negativo, pues ello no tiene sentido físico.