| |
|
| |
|
| |
La integral indefinida |
| |
|
|
"Si he conseguido ver más lejos, es porque me he aupado en hombros de gigantes.
No se lo que pareceré a los ojos del mundo,
pero a los míos es como si
hubiese sido un muchacho que juega en la orilla del mar
y se divierte de tanto en tanto encontrando un guijarro más pulido
o una concha más hermosa, mientras
el inmenso océano de la verdad se extendía, inexplorado frente a mi."
Isaac Newton
|
| |
|
| |
Hemos utilizado el proceso de integral definida para calcular áreas bajo la gráfica de alguna función y dentro de un intervalo determinado. Pero también vimos que el proceso de integración es el proceso inverso a la derivación. Al integrar una función f(x), o al encontrar su antiderivada, conseguimos la función F(x) para la que f(x) es derivada. |
| |
|
| |
Ahora trabajaremos sólo con el cálculo de antiderivadas, sin llegar a encontrar valores de áreas; esto es, daremos simplemente las expresiones de las antiderivadas de una función Para ello recordemos el siguiente teorema que abordamos antes: |
| |
|
| |
Si G’(x) = F’(x) para toda x en [a, b], entonces G(x) = F(x) + c para toda x en el intervalo. |
| |
|
| |
Es decir, dos antiderivadas de una misma función pueden diferir cuando mucho en una constante. |
| |
|
| |
Llamaremos integral indefinida al cálculo de la antiderivada de una función f(x). La notación de la integral indefinida es 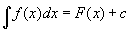 , donde a c se le conoce como constante de integración. , donde a c se le conoce como constante de integración. |
| |
|
| |
Fíjate que las diferencias con respecto a las integrales definidas son, por un lado, el hecho de que la integral indefinida carece de límites de integración, y por lo tanto NO SE EVALÚA, y por otro, que debe agregarse al resultado de la integral la constante de integración c. |
| |
|
| |
Por ejemplo, sabemos que la integral definida 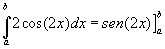 . De esta forma, la integral indefinida para la misma función será . De esta forma, la integral indefinida para la misma función será 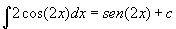 . . |
| |
|
| |
| |
|
|
|
|
|
 |
 |
|
|
|
|
| |
|
|
1/3 |
|
|
|
|
|
|
|
|
|