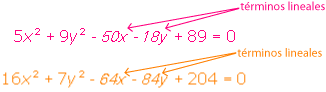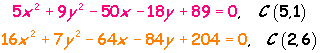Elipse: Los coeficientes hablan

Aquí puedes ver que las ecuaciones de elipses con centro en el origen tienen menos términos, pues sólo conservan los cuadráticos y el término independiente; los términos lineales valen cero y por eso no aparecen:

No hay términos lineales

No hay términos lineales

¿Puedes ver entonces dónde se encuentra la información del centro de una elipse? ¡Claro! ¡En los términos lineales! Así, cuando tengamos una ecuación sin ellos, querrá decir que su centro está en el origen. Ahora analicemos las ecuaciones en las que sí aparecen:

Observa con atención las ecuaciones para que contestes: ¿qué relación habrá entre cada término lineal y las coordenadas del centro? Te daremos una pista:

Para la abscisa del centro, debes encontrar una relación entre el coeficiente del término cuadrático x² y el coeficiente del término lineal x: ¿Cómo llegar a 5 en la primera ecuación, haciendo operaciones con los coeficientes 5 y -50? ¿Cómo llegar a 2 en la segunda ecuación, haciendo operaciones con los coeficientes 16 y -64?

La misma secuencia de operaciones que encuentres debe funcionar para las ordenadas: trabajando con 9 y -18 debemos llegar a 1 y con 7 y -84 debemos llegar a 6. Intenta encontrar la relación. Te damos una idea:

Revisa qué operaciones hiciste al desarrollar la ecuación para llegar a esos coeficientes. Cuando tengas tu propuesta, la hayas probado, y veas que funciona, arrastra la opción correcta para completar el texto.

Ahora que has verificado las respuestas, te sugerimos que leas todo el párrafo y pruebes si esta regla funciona. ¡Probemos!