Teorema Fundamental del Cálculo

Acabamos de ver que, así como anteriormente calculamos derivadas de funciones, también podemos calcular antiderivadas de funciones. También, en esta unidad, hemos aprendido procesos para calcular áreas bajo curvas y he hemos definido el proceso de integral. A continuación presentaremos un teorema que relacionará las antiderivadas, las integrales y las áreas bajo una curva.

Este teorema, al que llamaremos como Teorema Fundamental del Cálculo, será presentado de dos formas diferentes, ambas igualmente útiles. La primera de ellas se conoce como la forma de la derivada, mientras que la segunda se denomina la forma de antiderivada. Veamos la forma de la derivada.

Supongamos que tenemos una función f que es continua y que esta función no es negativa para cualquier valor t dentro de un intervalo [a, b]; es decir, f(t)≥0. Esto implica que la integral 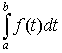 existe y representa el área bajo la gráfica de f en el intervalo [a, b].

Ahora, si x es cualquier valor en el intervalo [a, b], entonces la función A(x) = 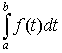 nos dará el área bajo la gráfica en el intervalo [a, x]. Resulta más claro en las siguientes gráficas:

Si tomamos un incremento en x, denotado por h y con h>0, entonces podemos escribir 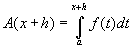. Las áreas bajo la gráfica para A(x + h) y para la diferencia de áreas establecida por A(x + h) – A(x) se muestran en las siguientes gráficas:

Ya que f es continua en [x, x + h], entonces adquiere un valor mínimo m y un valor máximo M en el intervalo. Dentro de este intervalo marcaremos primero el valor mínimo y generaremos un rectángulo de base h y altura m. Igualmente podemos generar un rectángulo de base h y altura M. Estas opciones se muestran en las gráficas:

De acuerdo a lo que podemos observar, la diferencia en las áreas denotada por A(x + h) – A(x) estará comprendida entre estas dos últimas superficies. Esto es 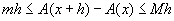. Si dividimos esta desigualdad entre h, tenemos que .

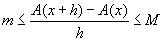Finalmente, sabemos que si hacemos tender la base h a cero, entonces las áreas de los dos rectángulos tenderán al área bajo la gráfica. Es decir, 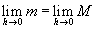, y además, por propiedades de las desigualdades, este valor será igual también a 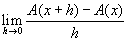, lo cual, por definición, es la derivada de A(x) o A’(x); a este límite, denotémoslo por f(x).

De esta forma, enunciamos el Teorema Fundamental del Cálculo en su forma de derivada como:
Sea f continua en [a, b] y sea x cualquier número en el intervalo. Si G(x) es la función definida por 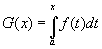, entonces G’(x) = f(x). Esto es, podemos decir ahora que la integral puede operar como el proceso inverso de la derivada o como el proceso de antiderivación.