| |
|
| |
|
| |
Máximos y mínimos y los signos de las tangentes |
| |
|
|
Encontramos que la función 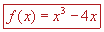 tiene dos valores críticos, tiene dos valores críticos,  y y 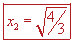 ; los cuales se obtuvieron a partir de igualar la primera derivada de la función con cero y resolver la ecuación resultante de este proceso. Pero el problema es que aún debemos saber si para estos valores críticos la función efectivamente toma valores máximos, mínimos, ambos o incluso ninguno. ; los cuales se obtuvieron a partir de igualar la primera derivada de la función con cero y resolver la ecuación resultante de este proceso. Pero el problema es que aún debemos saber si para estos valores críticos la función efectivamente toma valores máximos, mínimos, ambos o incluso ninguno. |
| |
|
| |
Para esto nos apoyaremos en la idea que acabamos de revisar en la animación pasada: las tangentes antes de un máximo son positivas, y después de él son negativas. Y las tangentes antes de un mínimo son negativas, y después de éste son positivas. |
| |
|
| |
Tomemos el valor crítico 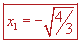 . Sabemos que ahí la pendiente de la tangente es cero; es decir . Sabemos que ahí la pendiente de la tangente es cero; es decir 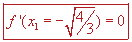 . Si revisamos las tangentes un poco antes de este valor de x y un poco después, tendremos la posibilidad de saber qué sucede con la función en ese valor en términos de máximos y mínimos. Si la tangente para un valor ligeramente menor es positiva y para un valor ligeramente mayor es negativa, entonces tendremos que la función toma un máximo en . Si revisamos las tangentes un poco antes de este valor de x y un poco después, tendremos la posibilidad de saber qué sucede con la función en ese valor en términos de máximos y mínimos. Si la tangente para un valor ligeramente menor es positiva y para un valor ligeramente mayor es negativa, entonces tendremos que la función toma un máximo en 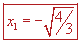 . Si sucede a la inversa, entonces tendremos un mínimo. . Si sucede a la inversa, entonces tendremos un mínimo. |
| |
|
| |
Y puede ocurrir que no haya un cambio de signo en las pendientes de las tangentes. En ese caso no habrá para ese punto ni un máximo ni un mínimo para la función. Pero ese tema será abordado más adelante. Como 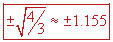 , evaluaremos , evaluaremos 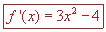 en -2 y en 0, que son los valores respectivamente menor y mayor al valor crítico: en -2 y en 0, que son los valores respectivamente menor y mayor al valor crítico: |
| |

|
| |

|
| |
|
| |
|
| |
|
| |
|