De forma determinada e indeterminada

Si al sustituir el valor  en una función  se obtiene  y se quiere calcular su límite cuando  se debe buscar una nueva función que sea igual a la función original pero que si tenga límite. Esto es en base al teorema que dice:

Para encontrar la función a la que sí se le pueda calcular su límite se aplican algunos métodos algebraicos los más utilizados son la factorización  y la racionalización. En la función que estamos trabajando procede la factorización y se aplica  de la siguiente forma:

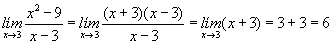
Puedes darte cuenta que esta forma algebraica te lleva a obtener el límite que ya habías obtenido por medio de su gráfica y de su tabla. Así es que deberás recordar los métodos de factorización y racionalización que estudiaste en tus cursos anteriores.