Términos lineales
   
 

Para una elipse horizontal, obtenemos la fórmula mediante la ecuación:

Si hacemos las operaciones necesarias para expresarla igualada a cero, tendremos:

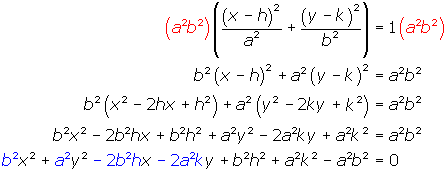
Si la ecuación general de una elipse (horizontal o vertical) se expresa como:
,

Para la elipse horizontal podemos hacer la siguiente equivalencia:

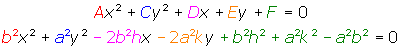
De allí que hagamos las siguientes afirmaciones:

  • El coeficiente de x2 es A=b2.
  • El coeficiente de x2 es A=b2.
  • El coeficiente del término lineal en x equivale a D=-2b2h, por lo que si de esa expresión despejamos h, tendremos 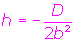 (¿te fijas que es lo que hacemos? Dividimos el coeficiente del término lineal en x entre el coeficiente de x2 , que en este caso vale b2 y luego dividimos entre -2.
  • El coeficiente del término lineal en y es E=-2a2k y por tanto .
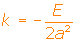  • Finalmente, el término independiente .

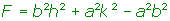El procedimiento para obtener las fórmulas para una elipse vertical es análogo, y se llega a que:
A=a2, B=b2, D=-2a2h y , E=-2b2k